Become a BST Ninja - Genin Level

Binary Search Tree (BST) is one of the most classic data structures. The definition for its structure is shown as below:

• It consists of Nodes and Leaves.
• A Node has a child bst on the left side, a key (, a data), and a child bst on the right side. Note here a node's left or right child is not a node, instead, is indeed another binary search tree.
• A Leaf has nothing but act only as a STOP sign.

type 'a bst_t =  
  | Leaf
  | Node of 'a bst_t * 'a * 'a bst_t (* Node (left, key, right) *)
(* a node may also carry a data associated with the key. 
   It is omitted here for neater demonstration *)

The important feature that makes BST unique is

• for any node
  • all keys from its left child are smaller than its own key
  • all keys from its right child are bigger (assumming keys are distinct)

And here is an example of BST:

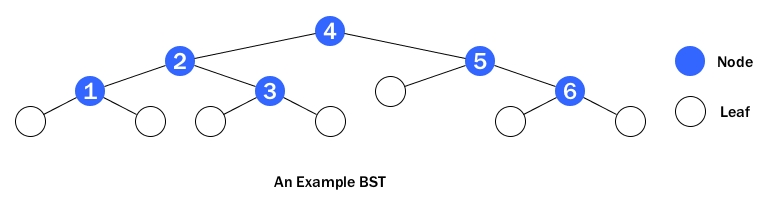
Instead of continuing to present the basics of BST, this post will now focus on how to attack BST related problems with the most powerful weapon: Recursion.

Recursion on BST

From Recursion Reloaded, we know that one way to model recursion is:

1. Assume we already got a problem solver: solve.
2. Don't think about what would happen in each iteration.
3. Split the problem to smallers sizes (N = N1 + N2 + ...).
4. Solve those smaller problems like solve N1, solve N2, ... Here is the tricky part: still, we do not know or care what are inside solve and how f would do the job, we just believe that it will return the correct results.
5. Now we have those results for smaller problems, how to wire them up to return the result for N? This is the ultimate question we need to answer.
6. Of course, we do not forget the STOP sign for some edge cases.
7. Together with point 5 and 6, we get our solve.

A good thing coming from BST is that the split step has been done already, i.e., a BST problem can be always divided into left child, root, and right child.

Thus if we assume we already got solve, we just need to solve left and / or solve right, then do something with root, and finally wire all outcomes to obtain the final result. Again, we should of course never forget the STOP sign and in BST, usually it is the Leaf, i.e., we need to ask ourselves what if the BST is a Leaf.

The thinking flow is illustrated as the diagram below.

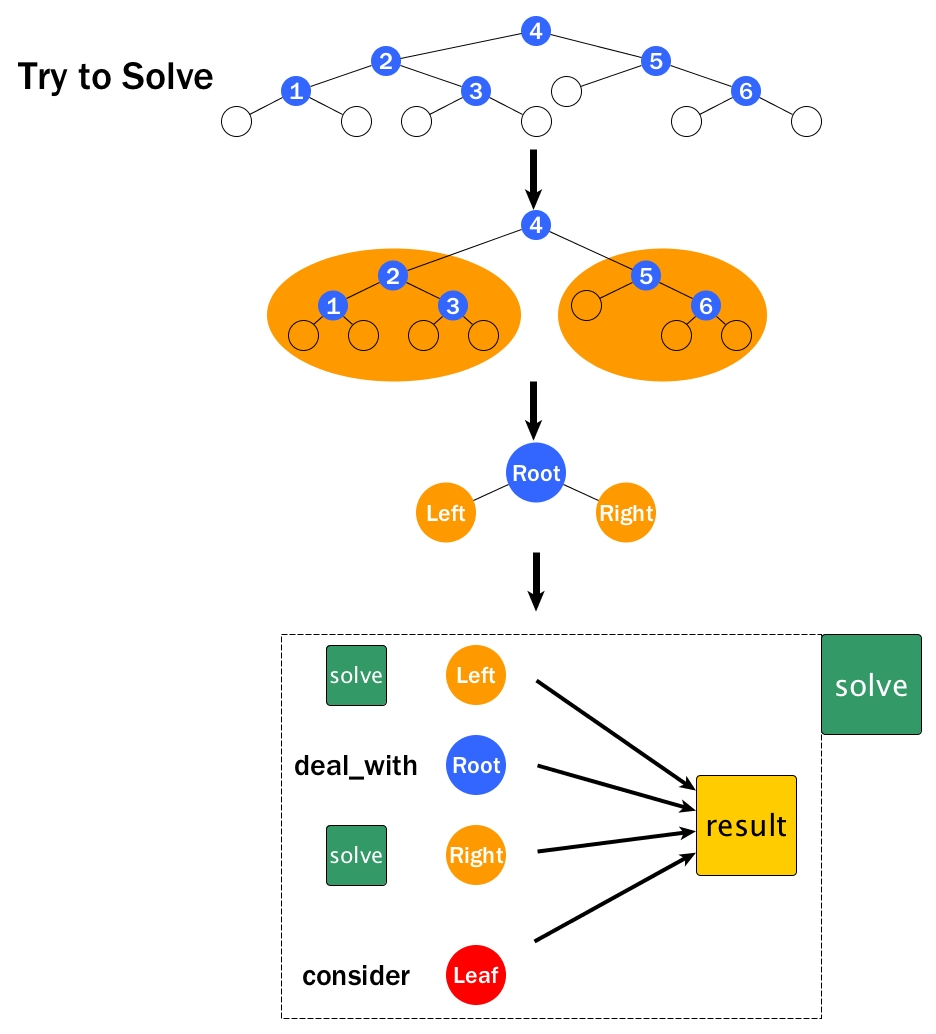
Before we start to look at some problems, note that in the diagram above or Recursion Reloaded, we seem to always solve both left and right, or say, all sub-problmes. It is actually not necessary. For BST, sometimes either left or right is enough. Let's have a look at this case first.

Either Left or Right

Our starter for this section is the simplest yet very essential operation: insert a key to a BST.

Insert

From the definition of BST, we know the basic rule is that if the new key is smaller than a root, then it belongs to the root's left child; otherwise, to the root's right child. Let's follow the modelling in the previous diagram to achieve this.

1. We assume we already got insert key bst
2. We know the problem can be split into left, root, and right.
3. Because a new key can go either left or right, so we need to deal_with root first, i.e., compare the new key and the key of the root.
4. Directly taken from the rule of BST, if the new key is smaller, then we need to solve left thus insert key left; otherwise insert key right.
5. What if we get to a Leaf? It means we can finally place our new key there as a new Node and of course, at this moment both children of the new Node are Leaves.

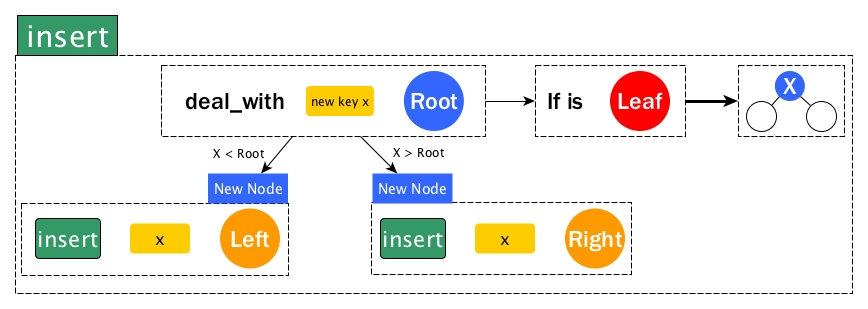
Note that the BST type in OCaml we defined early on is pure functional, which means every time we need to update something, we have to create new. That's why in the diagram, even if we just insert x to left or right, we need to construct a new Node because we are updating the left child or the right one. The code is shown as below.

let rec insert x = function  
  | Leaf -> Node (Leaf, x, Leaf) (* Leaf is a STOP *)
  | Node (left, k, right) ->
    if x < k then Node (insert x left, k, right) (* if x is smaller, go left *)
    else Node (left, k, insert x right) (* otherwise, go right *)

Member

member is to check whether a given key exists in the BST or not. It is very similar to insert. There are three differences:

1. When dealing with root, we need to see whether the given key equals to the root's key or not. If yes, then we hit it.
2. member is a readonly function, so we directly solve left or right without constructing new Node.
3. If arriving at a Leaf, then we have nowhere to go any more and it means the given key is not in the BST.

let rec mem x = function  
  | Leaf -> false
  | Node (left, k, right) ->
    if x < k then mem x left
    else if x = k then true
    else mem x right

Both Left and Right

Usually when we need to retrieve some properties of a BST or possibly go through all nodes to get an answer, we have to solve both children. However, the modelling technique does not change.

Height

Recall from Some properties of a tree, the height of a tree is the number of edges that the longest path (from the root to a leaf) has. From this definition, it seems easy to get the height. We simply try to find all possible paths from root and for each path we record its number of edges. The answer will be the max of them. It sounds straightforward, but if you really try to write the code in this way, I bet the code would be a bit messy. Honestly, I never wrote in this way and I will never do that.

Another way is to think recursively. First let analyse a little bit about the longest path matter.

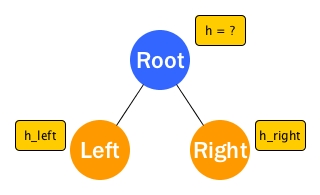
As we can see from the above diagram, Root has two edges: one to Left and the other to Right. So whatever the longest path from Root might be, it must pass either Left or Right. If we somehow could obtain the longest path from the root of Left and the longest path from the root of Right, the longest path from Root should be the bigger one of the two paths, right?

Let's now assume we already got height and it will return the height of a BST. Then we can obtain h_left and h_right. The answer is what is the h (height of Root)? Note that the height implies the longest path already (that's the definition). So from the paragraph above, What we need to do is getting max h_left h_right. Since Root has an edge to either child, h = 1 + max h_left h_right.

Don't forget the STOP sign: the height of a Leaf is 0.

let rec height = function  
  | Leaf -> 0
  | Node (left, _, right) -> 1 + max (height left) (height right)

Simple, isn't it?

Keys at a certain depth

So far, it seems our hypothetic solve function takes only the sub-probem as parameter. In many cases this is not enough. Sometimes we need to supply more arguments to help solve. For example, in the problem of retriving all keys at a certain depth definitely needs current depth information.

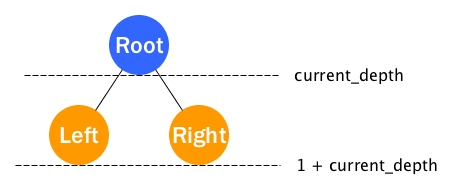
Only with the help of current_depth, the Root can know whether it belongs to the final results.

1. If current_depth = target_depth, then Root should be collected. Also we do not continue to solve Left or Right as we know their depths will never equal to target_deapth.
2. Otherwise, we need to solve both Left and Right with argument of 1 + current_depth.
3. Assume our solve is working. Then solve left (1+current_depth) would return a list of target nodes and so does solve right (1+current_depth). We simply then concatenate two target lists.
4. STOP sign: Leaf is not even a Node, so the result will be empty list.

The code is like this:

let rec from_depth d cur_d = function  
  | Leaf -> []
  | Node (left, k, right) ->
    if cur_d = d then [k]
    else from_depth d (cur_d + 1) left @ from_depth d (cur_d + 1) right

let all_keys_at depth bst = from_depth depth 0 bst  

Genin

From Ninja Wiki

A system of rank existed. A jōnin ("upper man") was the highest rank, representing the group and hiring out mercenaries. This is followed by the chūnin ("middle man"), assistants to the jōnin. At the bottom was the genin ("lower man"), field agents drawn from the lower class and assigned to carry out actual missions.

Ps.

Some readers contacted me. They hope that maybe I can use more advanced knowledge or harder examples in my posts and the current ones might seem a little boring. I think I need to explain a bit here.

The general idea behind Many things about OCaml is not to write a cookbook for certain problems related to OCaml or be a place where quick solution is there and copy / paste sample code would do the trick. Instead, Many things means some important aspects in OCaml that might be overlooked, or some particular problems that can show the greatness of OCaml, or the elegant OCaml solutions for some typical data structures and algorithms, etc. As long as something are valuable and that value shows only in OCaml or Functional Programming, I would like to add them all in here one by one.

Fortunately or unfortunately, even though I have only limited experiences in OCaml, I found that the many is actually quite big. And due to this many, I had to make a plan to present them all in a progressive way. Topics can interleave with each other in terms of time order as we do not want to have the same food for a month. More importantly, however, all should go from simple / easy to advanced / hard. In order to present some advanced topic, we need to make sure we have a solid foundation. This is why, for example, I even produced a post for the properties of a tree although they are so basic. This is also why I reloaded recursion since recursion is everywhere in OCaml. They are a kind of preparations.

Moreover, I believe in fundamentals. Fundamentals are normally concise and contain the true essence. But sometimes they can be easily overlooked or ignored and we may need to experience a certain number of difficult problems afterwards, then start to look back and appreciate the fundamentals.

The reason of using simple examples is that it makes my life easier for demonstrations. I love visualisations and one graph can be better than thousands of words. For complicated problems and solutions, it is a bit more difficult to draw a nice and clean diagram to show the true idea behind. I will try to do so later on, but even if I could achieve it in this early stage, some readers might easily get lost or confused because of the unavoidable complication of the graph. As a result, the point of grasping fundamentals might be missed.

Anyway, please don't worry too much. Attractive problems in OCaml are always there. For example, in my plan, I will later start to present a number (maybe 15 ~ 17) of my beloved Functional Pearls in OCaml and if you are really chasing for some awesomeness, I hope they would satisfy you.