Recursion Reloaded

One essential of computer programming is repeating some operations. This repetition has two forms: for / while loop and recursion.

Loop

• We directly setup a boundary via for or while.
• Certain conditions change inside the boundary.
• And operations are executed based on the changing conditions.
• It ends when hitting the boundary.

if asked to write the sum method in Java, it might be more intuitive to have this code:

/* Java */
public int sum(int[] a) {  
  int s = 0;
  for (int i = 1; i <= n; i++)
    s += a[i];
  return s
}

Recursion

• We write a function for the operations that need to be repeated.
• The repetition is achieved by invoking the function inside itself.
• We may not specify an explicit boundary, yet we still need to set a STOP sign inside the function to tell it when to stop invoking itself.
• It ends when hitting the STOP sign.

The recursive sum in OCaml can look like this:

(* OCaml *)
let sum = function  
  | [] -> 0 (*STOP sign*)
  | hd::tl -> hd + sum tl

loop or recursion?

In imperative programming, developers may use loop more often than recursion as it seems to be more straightforward.

However, in functional programming, we almost ([1]) cannot do loop, and recursion is our only option. The major reason is that loop always needs to maintain mutable states inside the clause to change the conditions or pass intermediate results through iterations. Unfortunately, in functional programming, mutables are not allowed ([2]) and also intermediates must be passed via function calls not state changing.

So, if we really wish to get into the OCaml world, we have to get used to recursion. If you feel a bit hard, then this post is supposed to help you a little bit and show you the lovely side of recursion.

Do you dislike recursion?

Honestly, I hated recursion in the beginning. In order to write a recursive function or validate one's correctness, I thought I had to always somehow simulate the execution flow in my head and imagine divings into one level after another and every time when I did that, my brain felt a bit lost after some levels and sometimes I had to use pen & paper.

This pain is natural. Human's brain feels much more comfortable on linear tasks than recursive ones. For example, if we are asked to finish the flow of first finish task-1 -> task-2 -> task-3 -> task-4 -> done, it seems concise and easy. On the other hand, if we are asked to finish task-1, inside which we need to finish task-2 and task-3, and inside task-2 we need to finish task-4 and task-5, and inside task-3 we need...([3]), our brain may not that happy, does it?

What is the difference between these two cases?

In the first case, when we do task-1, we do not need to care about task-2; and after we finish task-1, we just move on and forget task-2. Thus, we just focus and remember one thing at one time.

In the second case, when do do task-1, we not only need to foresee a bit on task-2 and task-3, but also can't forget task-1; and we need to still keep task-2 in mind after we begin task-4...

So the difference is very obvious: we remember / track more things in case 2 than in case 1.

Let's investigate this difference further in the paradigm of the two different sum functions written early.

Linear way

Summing [9;14;12;6;], what will we do?

1. We will do 9 + 14 first, we get 23 and we put the 23 somewhere, say, place S.
2. Next number is 12, then we check S, oh it is 23, so we do 23 + 12 and get 35.
3. Now, we do not need the previous result 23 any more and update S with 35.
4. Next one is 6, ...

If we look closer into the diagram above, we will find out that at any single step, we need to care only S and can forget anything happened before. For example, in step 1, we get 2 numbers from the list, calculate, store it to S and forget the 2 numbers; then go to step 2, we need to retrieve from S, get the 3rd number, then update S with new result and forget anything else...

Along the flow, we need to retrieve one number from the list at one time and forget it after done with it. We also need to remember / track S, but it is just a single place; even if its value changes, we do not care about its old value. In total, we just have to bear 2 things in mind at all time, no matter the how big the list can be.

For a contrast, let's take a look at the recursive way.

Recursive way

If we try to analyse the recursive sum, we get

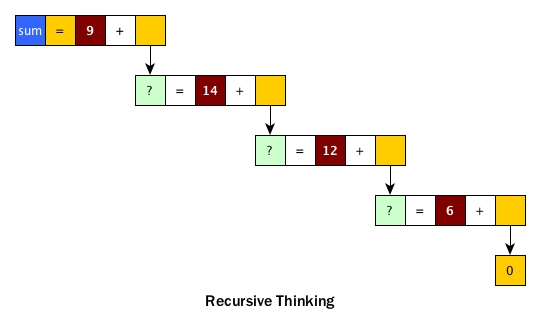
After we retrieve the first number, 9, from the list, we cannot do anything yet and have to continue to retrieve 14 without forgetting 9, and so on so forth. It is easy to see that we need to remember 4 things (marked as red square) if we use our brain to track the flow. It might be fine if there are only 4 numbers. Yet if the list has 100 random numbers, we need to remember 100 things and our brains would be fried.

Basically, as long as we try to simulate the complete recursive / iteration flow, we cannot avoid remembering potentially big number of things. So what is the solution to escape this pain? The answer is simple: we do not simulate.

Actually, for many problems that need recursion, we do not need to look into the details of recursion and we do not need to iterate the function in our heads. The trick is the way of modeling the recursion.

Recursion should be loved

Let's revise the recursive sum function:

let sum = function  
  | [] -> 0 (*STOP sign*)
  | hd::tl -> hd + sum tl

One bad way to interpret its repeatition process is

1. We get an element out
2. On the lefthand side of +, we hold it
3. On the righthand side of +, we do point 1 again.
4. After STOP, we do the plus on the previous numbers that were held, one by one

This way is bad because it involves simulating the flow.

The good way to interpret is:

1. Someone tells me sum can do the job of summing a list
2. We don't care what exactly sum is doing
3. If you give me a list and ask me to sum, then I just get the head (hd) out, and add it with sum of the rest
4. Of course, what if the list is empty, then sum should return 0

Unlike the bad way, this modelling has actually removed the iteration part from recursion, and been purely based on logic level: sum of list = hd + sum of rest.

To summary this process of modelling:

• I need to write a recursive function f to solve a problem
• I won't think the exact steps or details inside f
• I just assume f is already there and correct
• If the problem size is N, then I divide it into X and Y where X + Y = N
• If f is correct, then f X and f Y are both correct, right?
• So to solve N, we just need to do f X and f Y, then think out some specific operations to wire the results together.
• Of course, f should recognise STOP signs.

So what we really need to do for recursion are:

1. Think how to divid N to X and Y
2. Think how to deal with the results from f X and f Y in order to get result of f N
3. Set the STOP sign(s)

Let's rewrite sum to fully demenstrate it

1. We need to sum a list
2. I don't know how to write sum, but I don't care and just assume sum is there
3. a list l can be divid to [hd] + tl
4. So sum l = sum [hd] + sum tl should make sense.
5. Of course, STOP signs here can be two: sum [] = 0 and sum [x] = x.

let sum = function  
  | [] -> 0 (*STOP sign*) 
  | [x] -> x (*STOP sign*)
  | hd::tl -> sum [hd] + sum tl (* Logic *)
(* note sum [hd] can directly be hd, I rewrote in this way to be consistent to the modelling *)

I am not sure I express this high level logic based modelling clearly or not, but anyway we need more practices.

Merge two sorted lists

We need a merge function to merge two sorted lists so the output list is a combined sorted list.

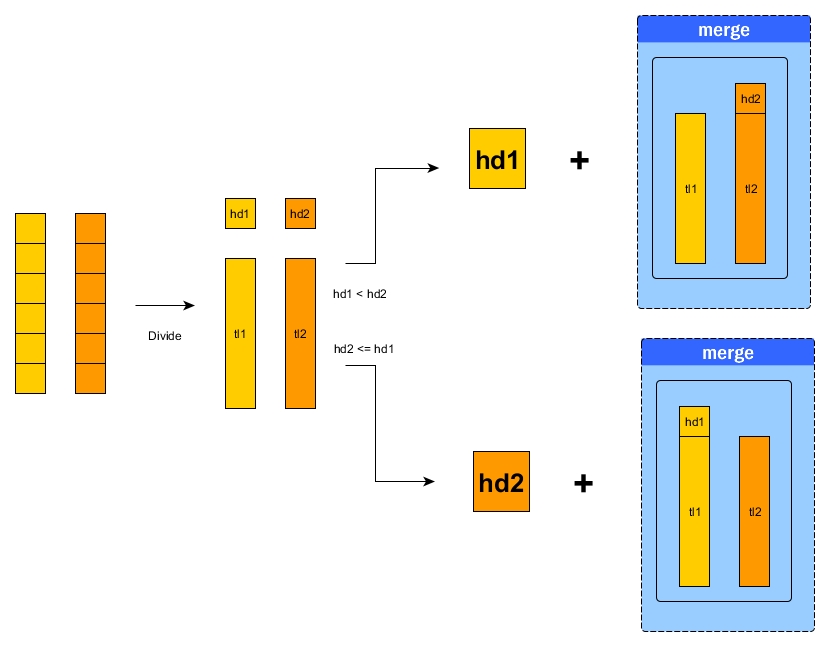
N = X + Y

Because the head of the final combined list should be always min, so we care about the first elements from two lists as each is already the min inside its owner. l1 = hd1 + tl1 and l2 = hd2 + tl2.

f N = wire (f X) (f Y)

We will have two cases here.

If hd1 < hd2, then X = tl1 and Y = l2, then the wiring operation is just to add hd1 as the head of merge X Y

If hd1 >= hd2, then X = l1 and Y = tl2, then the wiring operation is just to add hd2 as the head of merge X Y

STOP sign

If one of the lists is empty, then just return the other (no matter it is empty or not).

Code

Then it should be easy to write the code from the above modelling.

let merge = function  
  | [], l | l, [] -> l (*STOP sign, always written as first*) 
  | hd1::tl1 as l1, hd2::tl2 as l2 -> 
    if hd1 < hd2 then hd1::merge (tl1, l2)
    else hd2::merge (l1, tl2)

The idea can be demonstrated by the diagram below:

Mergesort

Mergesort is a way to sort a list.

N = X + Y

We can split N evenly so X = N / 2 and Y = N - N / 2.

f N = wire (f X) (f Y)

What if we already mergesorted X and mergesorted Y? We simply merge the two results, right?

STOP sign

If the list has just 0 or 1 element, we simply don't do anything but return.

Code

(* split_evenly is actually recursive too
   We here just ignore the details and use List.fold_left *)
let split_evenly l = List.fold_left ~f:(fun (l1, l2) x -> (l2, x::l1)) ~init:([], []) l

let rec mergesort l =  
  match l with
    | [] | hd::[] as l -> l
    | _ -> 
      let l1, l2 = split_evenly l in
      merge (mergesort l1) (mergesort l2)

More recursions will follow

So far, all examples used in this post are quite trivial and easy. I chose these easy ones because I wish to present the idea in the simplest way. Many other recursion problems are more complicated, such as permutations, combinations, etc. I will write more posts for those.

One of the execellent use case of recursion is Binary Search Tree. In BST, we will see that the size of a problems is naturally split into 3. Depending on the goal, we deal with all or partial of the 3 sub-problems. I will demonstrate all these in the next post.

Again, remember, when dealing with recursion, don't try to follow the execution flow. Instead, focus on splitting the problem into smaller ones and try to combine the results. This is also called divide and conquer and actually it is the true nature of recursion. After all, no matter the size of the problem can be, it is anyway the same function that solve the cases of size = 0, size = 1, and size = n > 2, right?

[1] OCaml allows imperative style, but it is not encouraged. We should use imperative programming in OCaml only if we have to.

[2] OCaml allows mutables and sometimes they are useful in some cases like in lazy or memorise. However, in most cases, we are not encouraged to use mutables.

[3] I already got lost even when I am trying to design this case