Height, Depth and Level of a Tree

This is a post on the three important properties of trees: height, depth and level, together with edge and path. I bet that most people already know what they are and tree (data structure) on wiki also explains them briefly.
The reason why I still decided to produce such a trivial page is that I will later on write a series of articles focusing on binary search tree in OCaml. The starters among them will be quite basic and related to these three properties.
In order to be less boring, the properties are presented in a visual way and I try to fulfill details (some might be easily overlooked) as much as possible.
Edge
Edge – connection between one node to another.
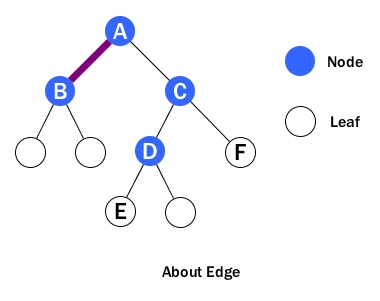
An example of edge is shown above between A and B. Basically, an edge is a line between two nodes, or a node and a leaf.
Path
Path – a sequence of nodes and edges connecting a node with a descendant.
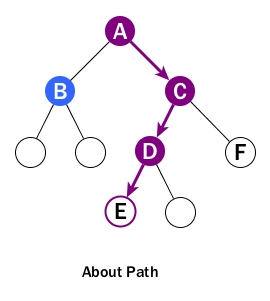
A path starts from a node and ends at another node or a leaf. Please don't look over the following points:
- When we talk about a path, it includes all nodes and all edges along the path, not just edges.
- The direction of a path is strictly from top to bottom and cannot be changed in middle. In the diagram, we can't really talk about a path from B to F although B is above F. Also there will be no path starting from a leaf or from a child node to a parent node. ([1])
Height
Height of node – The height of a node is the number of edges on the longest downward path between that node and a leaf.
At first, we can see the above wiki definition has a redundant term - downward - inside. As we already know from previous section, path can only be downward.
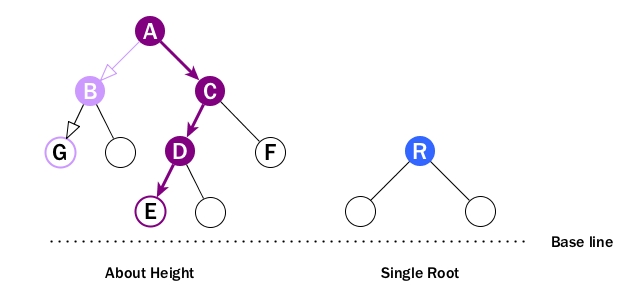
When looking at height:
- Every node has height. So B can have height, so does A, C and D.
- Leaf cannot have height as there will be no path starting from a leaf.
- It is the longest path from the node to a leaf. So A's height is the number of edges of the path to E, NOT to G. And its height is 3.
The height of the root is 1.
Height of tree –The height of a tree is the number of edges on the longest downward path between the root and a leaf.
So the height of a tree is the height of its root.
Frequently, we may be asked the question: what is the max number of nodes a tree can have if the height of the tree is h?. Of course the answer is $ 2^h-1 $ . When $ h = 1 $ , the number of node inside is 1, which is just the root; also when a tree has just root, the height of the root is 1. Hence, the two inductions match.
How about giving a height of 0? Then it means we don't have any node in the tree; but still we may have leaf inside (note that in this case we may not call it root of the tree as it makes not much sense). This is why in most languages, the type of a tree can be a leaf alone.
type 'a bst =
| Leaf
| Node of 'a bst * 'a * 'a bst
Moreover, when we use $2^h-1$ to calculate the max number of nodes, leaves are not taken into account. Leaf is not Node. It carries no key or data, and acts only like a STOP sign. We need to remember this when we deal with properties of trees.
Depth
Depth –The depth of a node is the number of edges from the node to the tree's root node.
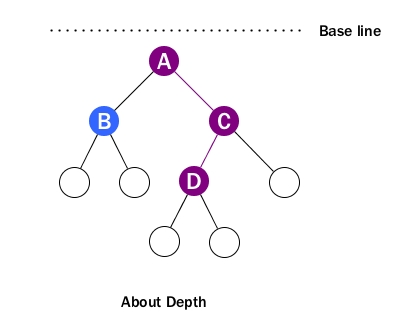
We don't care about path any more when depth pops in. We just count how many edges between the targeting node and the root, ignoring directions. For example, D's depth is 2.
Recall that when talking about height, we actually imply a baseline located at bottom. For depath, the baseline is at top which is root level. That's why we call it depth.
Note that the depth of the root is 0.
Level
Level – The level of a node is defined by 1 + the number of connections between the node and the root.
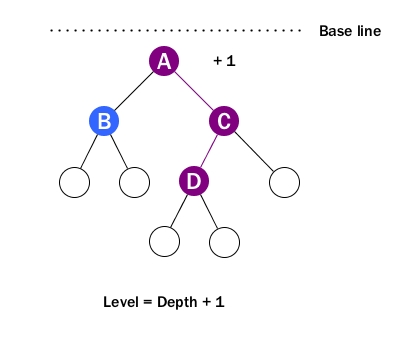
Simply, level is depth plus 1.
The important thing to remember is when talking about level, it starts from 1 and the level of the root is 1. We need to be careful about this when solving problems related to level.
[1] Although point 2 stands, sometimes some problems may talk about paths in an arbitrary way, like the path between B and F. We have to live with that while deep in our hearts remembering the precise definition.
ps. yEd - Graph Editor has been used to create all diagrams here.