Permutations

In this post, we will talk about producing permuations using OCaml. Generating permutations was actually one of my first self-homeworks when I started to learn OCaml years ago. It can be a good exercise to train our skills on list, recursion, foundamental fold, map, etc, in OCaml. Also it shows the conciseness of the OCaml as a language.

We will first present 2 common approaches for generating all permutations of a list of elements.

Then we introduce the Johnson Trotter algorithm which enable us to generate one permutation at a time.

Although Johnson Trotter algorithm uses imperative array, it provides us the opportunity to implement a stream (using stream list or built-in Stream module) of permutations, i.e., we generate a permutation only when we need. We will describe that as last.

The insert-into-all-positions solution

We can generate permutations using recursion technique. As we descriped in Recursion Reloaded, let's first assume we already get a function that can produce all permuations.

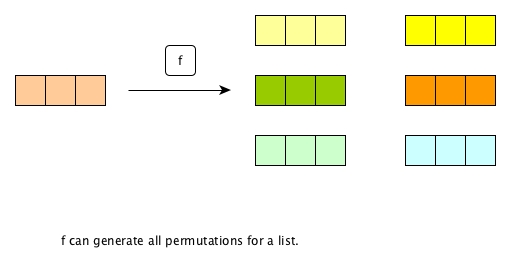
What exactly f will generate is not our concern for now, but we are sure that given a list (say 3 distinct elements), f will produce a list of permutations (totally 6 in this example).

So now what if our original list has one more new element?

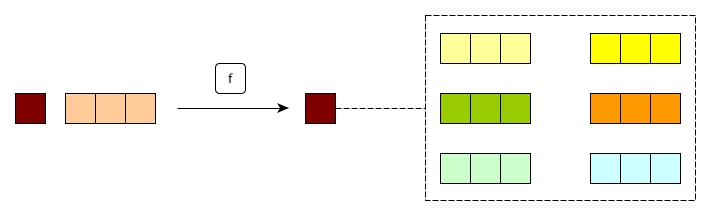
What should we do to combine the new element together with the old list of permutations, in order to generate a new list of permuatations?

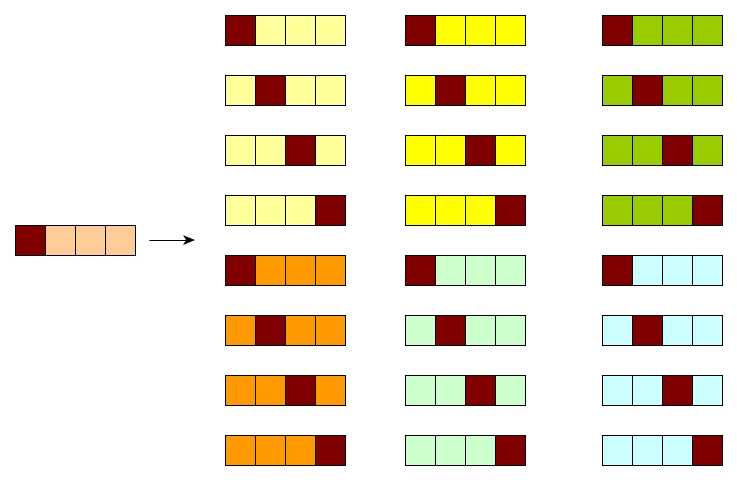
Let's first take a look at how to combine the new element with one permutation.

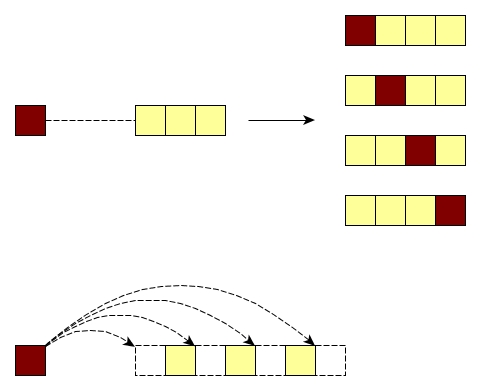
A good way, like shown above, is to insert the new element into all possible positions. Easy, right?

So for the new list of permutations, we just insert the new element into all possible positions of all old permutations.

code

First let's implement the function that combines an element with a permutation (which is actually a normal list).

(* note that in order to preserve certain order and also show the conciseness of the implementation, no tail-recursive is used *)
let ins_all_positions x l =  
  let rec aux prev acc = function
    | [] -> (prev @ [x]) :: acc |> List.rev
    | hd::tl as l -> aux (prev @ [hd]) ((prev @ [x] @ l) :: acc) tl
  in
  aux [] [] l

Now the main permutations generator.

let rec permutations = function  
  | [] -> []
  | x::[] -> [[x]] (* we must specify this edge case *)
  | x::xs -> List.fold_left (fun acc p -> acc @ ins_all_positions x p ) [] (permutations xs)

Here is the Gist.

The fixed-head solution

There is another way to look at the permutations.

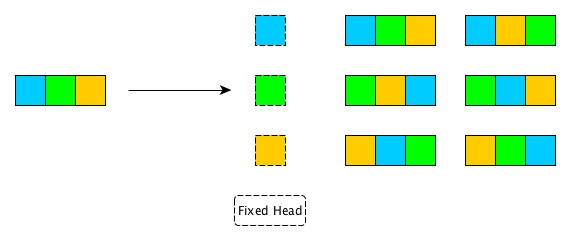
For a list of 3 elements, each element can be the head of all permutations of the rest elements. For example, blue is the head of the permutations of green and yellow.

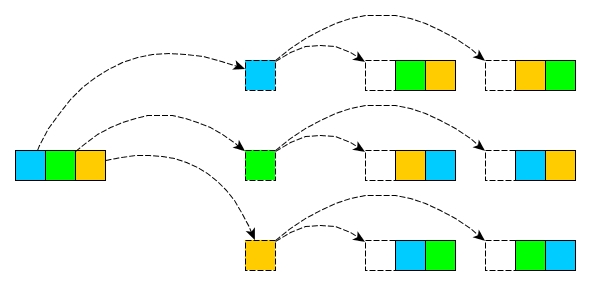
So what we can do is

1. Get an element out
2. Generate all permutations on all other elements
3. Stick the element as the head of every permutation
4. We repeat all above until we all elements have got their chances to be heads

Code

First we need a function to remove an element from a list.

let rm x l = List.filter ((<>) x) l  

The rm above is not a must, but it will make the meaning of our following permutations clearer.

let rec permutations = function  
  | [] -> []
  | x::[] -> [[x]]
  | l -> 
    List.fold_left (fun acc x -> acc @ List.map (fun p -> x::p) (permutations (rm x l))) [] l

(* The List.fold_left makes every element have their oppotunities to be a head *)

Here is the Gist

No tail-recusive?

So far in all our previous posts, the tail-recusive has always been considered in the codes. However, when we talk about permutations, tail-recusive has been ignored. There are two reasons:

At first, it is not possible to make recusion tail-recusive everywhere for the two solutions. The best we can do is just make certain parts tail-recusive.

Secondly, permutation generation is a P problem and it is slow. If one tries to generate all permutations at once for a huge list, it would not be that feasible. Thus, when talking about permutations here, it is assumed that no long list would be given as an argument; hence, we assume no stackoverflow would ever occur.

In addition, ignoring tail-recusive makes the code cleaner.

What if the list is huge?

If a list is huge indeed and we have to somehow use possibly all its permutations, then we can think of making the permutations as a stream.

Each time we just generate one permutation, and then we apply our somewhat use_permuatation function. If we need to continue, then we ask the stream to give us one more permutation. If we get what we want in the middle, then we don't need to generate more permutations and time is saved.

If we still have to go through all the permutations, time-wise the process will still cost us much. However, we are able to avoid putting all permutations in the memory or potentiall stackoverflow.

In order to achieve a stream of permutations, we need Johnson Trotter algorithm and a stream.

Johnson Trotter algorithm

The advantage of this algorithm is its ability to generate a new permutation based on the previous one, via simple O(n) operations (the very first permutation is the list itself). This is ideal for our adoption of stream.

The disadvantage, epecially for OCaml, is that it needs an mutable array. Fortunately, we can encapsulate the array in a module or inside a function, without exposing it to the outside world. Thus, certain level of safety will be maintained.

Personally I think this algorithm is very clever. Johnson must have spent quit much time on observing the changes through all permutations and set a group of well defined laws to make the changes happen naturally.

An assumption - sorted

The first assumption of this algorithm is that the array of elements are initially sorted in ascending order ([1]).

If in some context we cannot sort the original array, then we can attach additional keys, such as simple integers starting from 1, to every element. And carry on the algorithm based on that key.

For example, if we have [|e1; e2; e3; e4|] and we do not want to sort it, then we just put an integer in front of each element like [|(1, e1); (2, e2); (3, e3); (4, e4)|]. All the following process can target on the key, and only when return a permutation, we output the e in the tuple.

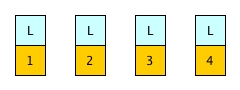
For simplicity, we will have an example array [|1; 2; 3; 4|], which is already sorted.

Direction: L or R

The key idea behind the algorithm is to move an element (or say, switch two elements) at a time and after the switching, we get our new permutation.

For any element, it might be able to move either Left or Right, i.e., switch position with either Left neighbour or Right one.

So we will attach a direction - L (initially) or R - to every element.

Movable

Even if an element has a direction, it might be able to move towards that direction. Only if the element has a smaller neighbour on that direction, it can move.

For example,

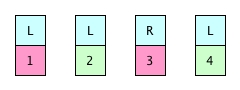
4 and 2 are movable, because the neighbours on their left are smaller.

3 is not movable, because 4 is not smaller.

1 is not movable, because it doesn't have any neighbour on its left.

Scan for largest movable element

As we described before, the algorithm makes a new permutation by moving an element, i.e., switch an element with the neighbour on its direction.

What if there are more than one elmeent is movable? We will choose the largest one.

Each time, when we are about to generate a new permutation, we simply scan the array, find the largest movable element, and move it.

If we cannot find such an element, it means we have generated all possible permutations and we can end now.

For example,

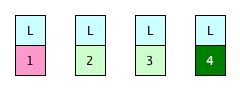
Although in the above case, 2, 3 and 4 are all movable, we will move only 4 since it is largest.

The whole process will end if no element is movable.

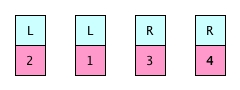
Note that this scan is before the movement.

Scan to flip directions of larger element

After we make a movement, immediately we need to scan the whole array and flip the directions of elements that are larger than the element which is just moved.

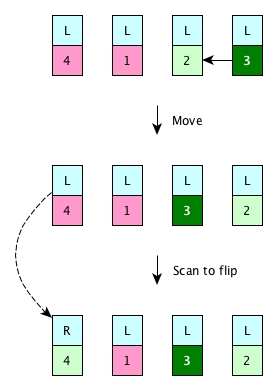
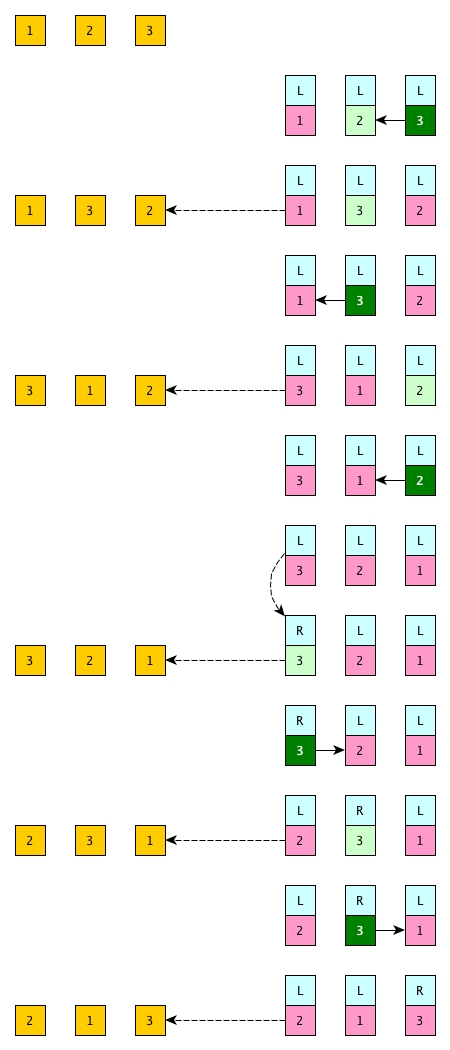
A complete example

Code

Direction

type direction = L | R

let attach_direction a = Array.map (fun x -> (x, L)) a

Move

let swap a i j = let tmp = a.(j) in a.(j) <- a.(i); a.(i) <- tmp

let is_movable a i =  
  let x,d = a.(i) in
  match d with
    | L -> if i > 0 && x > (fst a.(i-1)) then true else false
    | R -> if i < Array.length a - 1 && x > (fst a.(i+1)) then true else false

let move a i =  
  let x,d = a.(i) in
  if is_movable a i then 
    match d with
      | L -> swap a i (i-1)
      | R -> swap a i (i+1)
  else
    failwith "not movable"

Scan for the larget movable element

let scan_movable_largest a =  
  let rec aux acc i =
    if i >= Array.length a then acc
    else if not (is_movable a i) then aux acc (i+1)
    else
      let x,_ = a.(i) in
      match acc with
        | None -> aux (Some i) (i+1)
        | Some j -> aux (if x < fst(a.(j)) then acc else Some i) (i+1)
  in
  aux None 0

Scan to flip larger

let flip = function | L -> R | R -> L

let scan_flip_larger x a =  
  Array.iteri (fun i (y, d) -> if y > x then a.(i) <- y,flip d) a

Permutations generator

let permutations_generator l =  
  let a = Array.of_list l |> attach_direction in
  let r = ref (Some l) in
  let next () = 
    let p = !r in
    (match scan_movable_largest a with (* find largest movable *)
      | None -> r := None (* no more permutations *)
      | Some i -> 
        let x, _ = a.(i) in (
        move a i; (* move *)
        scan_flip_larger x a; (* after move, scan to flip *)
        r := Some (Array.map fst a |> Array.to_list)));
    p
  in
  next

(* an example of permutation generator of [1;2;3].
   Every time called, generator() will give either next permutation or None*)
let generator = permutations_generator [1;2;3]

> generator();;
> Some [1; 2; 3]

> generator();;
> Some [1; 3; 2]

> generator();;
> Some [3; 1; 2]

> generator();;
> Some [3; 2; 1]

> generator();;
> Some [2; 3; 1]

> generator();;
> Some [2; 1; 3]

> generator();;
> None

Here is the Gist.

The imperative part inside

Like said before, although we use array and ref for the impelmentation, we can hide them from the interface permutations_generator. This makes our code less fragile, which is good. However, for OCaml code having imperative parts, we should not forget to put Mutex locks for thread safety.

A stream of permutations

Now it is fairly easy to produce a stream of permutations via built-in Stream.

let stream_of_permutations l =  
  let generator = permutations_generator l in
  Stream.from (fun _ -> generator())

[1]. The array can be descending order, which means later on we need to put all initial directions as R.