Immutable

In pure functional programming, everything is immutable. Strings, lists, values of customised types etc cannot be changed once being created. For example, a list such as [1;2;3] does not have any operation that can alter its elements. If you want the stuff inside to be changed, you need to create a new list based on it. Suppose you want to change the first element of [1;2;3] to be 4, then you have to let new_list = 4::List.tl [1;2;3] or directly let new_list = [4;2;3], however, you don't have ways to do something like old_list.first_element = 4.

If you have got used to popular imperative programming languages such C, Java, Python, etc, you may feel that things being immutable sounds quite inconvenient. Yes, maybe sometimes being immutable forces us to do more things. In the example above, if we are able to do old_list.first_element = 4, it seems more natural and straightforward. However, please do not overlook the power of being immutable. It provides us extra safety, and more importantly, it leads to a different paradigm - functional programming style.

Before we start to dive into immutables, there are two things that need to be clarified first.

Shadowing

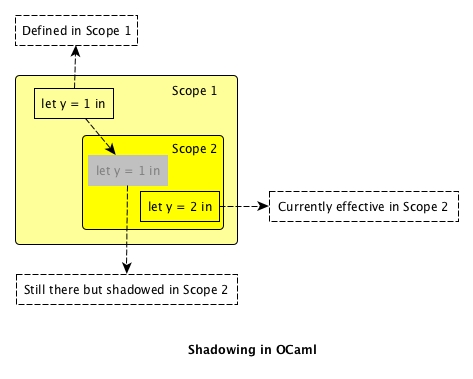
People who start to learn OCaml may see something, like the trivial code below, is allowed:

let f x =  
  let y = 1 in
  let y = 2 in
  x * y

There are two ys and it seems that y has been changed from 1 to 2. A conclusion might be made that things in OCaml are actually mutable because y is mutated. This conclusion is wrong. In OCaml, it is called shadowing.

Basically, the two ys are different. After the binding of second y is defined, the first y is still there for the time being. Just because it happens to have the same name as second y, it is in the shadow and can never be accessed later in the term of scope. Thus we should not say y is mutated and in OCaml variable / binding is indeed immutable.

Mutable Variables and Values

The concept of being immutable or mutable was introduced because we need it to help us to predict whether something's possible change would affect other related things or not. In this section, we majorly talk about mutable in imperative programming as clear understading of what being mutable means can help us appreciate immutable a little more.

It is easy to know variable is mutable in imperative programming. For example, we can do int i = 0;, then i = 1; and the same i is mutated. Altering a variable can affect other parts in the program, and it can be demonstrated using a for loop example:

/* The *for* scope repeatedly access `i` 
   and `i`'s change will affect each iteration. */

for (int i = 0; i < 10; i++)  
  System.out.println(i);

Sometimes, even if a variable is mutated, it might not affect anything, like the example (in Java) below:

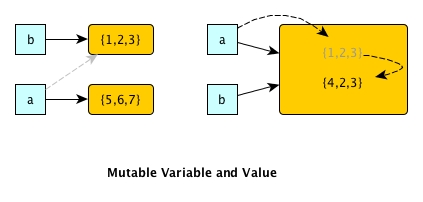
int[] a = {1;2;3};  
int[] b = a;

a = {5;6;7};

/* What is b now? */

a was initially {1,2,3}. b has been declared to be equal to a so b has the same value as {1,2,3}. a later on was changed to {5,6,7}. Should b be changed to {5,6,7} as well? Of course not, b still remains as {1,2,3}. Thus, even if a is mutated, b is not affected. This is because in this case, the value underneath has not been mutated. Let's modify the code a little bit:

int[] a = {1,2,3};  
int[] b = a;

a[0] = 0;

/* What is b now? */

a[0] = 0; altered the first element in the underlying array and a would become {0,2,3}. Since array in Java is mutable, b now becomes {0,2,3} too as b was assigned the identical array as a had initially. So the array value being mutable can lead to the case where if a mutable value is changed somewhere, all places that access it will be affected.

A mutable value must provide a way for developers to alter itself through bindings, such as a[0] = 0; is the way for arrays, i.e., via a[index] developers can access the array a by index and = can directly assign the new element at that index in the array.

A immutable value does not provide such as way. We can check immutable type String in Java to confirm this.

To summarise, when dealing with mutable, especially when we test our imperative code, we should not forget possible changes of both variable and value.

Note that OCaml does support mutable and it is a kind of hybrid of functional and imperative. However, we really should care about the functional side of OCaml more. For the imperative style of OCaml and when to use it, the next post will cover with details.

Extra Safety from Immutable

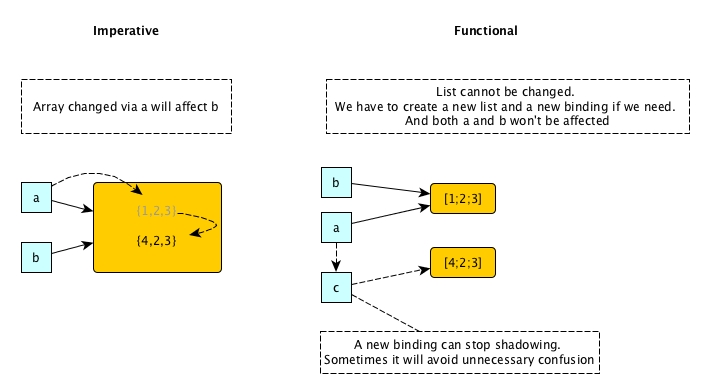
As described before, if a mutable variable / value is altered in one place, we need to be cautious about all other places that may have access to it. The code of altering an array in the previous section is an example. Another example is supplying a mutable value to a method as argument.

public static int getMedian(int[] a) {  
    Arrays.sort(a);
    return a[a.length/2];
}

public static void main(String[] args) {  
    int[] x = {3,4,2,1,5,9,6};
    int median = getMedian(x);

    /* x is not {3,4,2,1,5,9,6} any more */
    ...
}

getMedian will sort the supplied argument and the order of the elements in x will be changed after the call. If we need x to always maintain the original order, then the above code has serious flaw. It is not that bad if it is us who wrote getMedian, because we can just refine the code directly. However, if getMedian is in a third party library, even though we still can override this method, how can we know whether other method in the same library have this kind of flaw or not? A library would be useless if we cannot trust it completely.

Allowing mutables also introduces troubles for threading. When multiple threads try to alter a mutable value at the same time, we sometimes can just put a locker there to restrain the access to the value, with the sacrifice of make it single-threading at that point. However, if we have to precisely control the order of altering, things get much more complicated. This is why we have hundreds of books and articles to teach how to do a great multithreading in imperative programming languages.

If everything is immutable, then we do not need to worry about any of those any more. When we need to alter an immutable value, we create a new value that implements the change based on the old value and the old value is kept intact. All places that need access to the original value are very safe. As an example in OCaml:

(* trivial way to get median in OCaml, simply for comparison to the imperative case *)
let get_median l =  
  (* we can't sort in place, have to return a new sorted list *)
  let sorted_l = List.sort compare l in
  let len = List.length l in
  List.nth (len/2) sorted_l (* here we use our new sorted list *)

let median_mul_hd =  
  let l = [3;4;2;1;5;9;6] in
  let median = get_median l in
  median * List.hd l (* the hd of l will not be 1, but still 3 - the original hd *)

With immutables, the burden of cautions on unexpected modification of values are relieved for us. Hence, for OCaml, we do not need to spend time on studying materials such as Item 39: Make defensive copies when needed in Effective Java.

Being immutable brings extra safety to our code and helps us to avoid possibly many trivial bugs like the ones described before. However, this is not free of charge. We may feel more restrictive and lose much flexibilities ([1]). Moreover, because we cannot alter anything, pure functional programming forces us to adapt to a new style, which will be illustrated next.

Functional Programming Style

As mentioned in Recursion Reloaded, we cannot use loops such in pure functional programming, because mutable is not in functional world. Actually, there was a little misinterpretation there: it is not we cannot but is we are not able to.

A typical while loop in Java looks like this:

int i = 0;  
while ( i < 10 ) {  
   ...
   i++;
}

/* note that above is the same as
   for(int i = 0; i < n; i++) ... */

The reason that the while loop works in Java is because:

1. i is defined before while scope.
2. We go into while scope and i continues to be valid inside.
3. Since i is mutable, i's change is also valid inside while.
4. So we can check the same i again and again, and also use it repeatedly inside while.

Are we able to do the same thing in OCaml / Functional Programming? The answer is no.If you are not convinced, then we can try to assume we were able to and fake some OCaml syntax.

(* fake OCaml code *)

let i = 0 in  
while i < 10 do  
  ...
  let i = i + 1 ...
end while

1. i is defined before while, no problem.
2. Initially, while gets i for the first time and check it against 10, no problem.
3. i can be used for the first time inside ..., still no problem.
4. Then we need to increase i and the problem starts.
5. Recall that i is immutable in OCaml. The first i after let in let i = i + 1 is actually new and the original i is shadowed.
6. The new i is created within the while scope, so after one iteration, it is invalid any more.
7. Thus the second time at while i < 10 do, the original i would be still 0 and the loop would stuck there forever.

The above attempt proves that we can't do looping in pure functional programming any more. This is why we replace it with recursion as described in Recursion Reloaded before.

Furthermore, we can see that the execution runtime in imperative programming is normally driven by mutating states (like the while loop gets running by changing i). In functional programming, however, the execution continues by creating new things and giving them to the next call / expression / function. Just like in recursion, a state needs to be changed, so we give the same function the new state as argument. This is indeed the functional programming style: we create and then deliver.

One may still think imperative is easier and more straightforward than functional. Our brain likes change and forget, so for imperative's easiness, maybe. However, if you say imperative is more straightforward, I doubt it.

Let's temporarily forget the programming / coding part and just have a look at something at high level.

Suppose there is process, in which there are two states: A and B. Most importantly, State A can change to State B. Now plese close your eyes and draw a diagram for this simple process in your mind.

Done?

I bet you imagined this diagram as below:

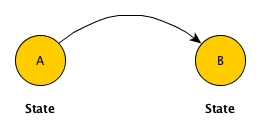
But NOT

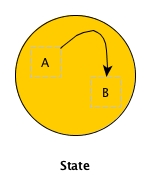
When we were really thinking of the trivial process, there must be two separate states in our mind and an explicit arrow would be there to clearly indicate the transition. This is much more nature than imagining just one state and the two situations inside. Afterall, this is called landscape and we often need it when we design something.

When we start to implement it, we might think differently. We sometimes intend to use the easy way we get used to. For example, in many cases we can just use one state variable and forget State A after transiting to State B during implementation, because always remembering State A may be unnecessary. This difference between design and implementation are always there and we are just not aware of it or we just feel it smoother due to our imperative habit.

Functional programming style does not have that difference. In the above example, if we implement it in OCaml, we will do exactly the same as the upper diagram, i.e., we create State A and when the state needs to be changed to B, we create a new State B. This is why I say functional is more straightforward because it directly reflects our intuitive design. If you are not convinced still, let's design and implement the quicksort in both imperative and functional styles as an demonstration.

Quicksort

Quicksort is a classic sorting algorithm.

1. If only one or no element is there, then we are done.
2. Everytime we select a pivot element, e.g. the first element, from all elements that we need to sort.
3. We compare elements with the pivot, put the smaller elements on its left hand side and larger ones on its right hand side. Note that neither smallers or largers need to be in order.
4. The pivot then gets fixed.
5. Quicksort all elements on its left.
6. Quicksort all elements on its right.

The core idea of quicksort is that we partition all elements into 3 parts: smaller, pivot and larger in every iteration. So smaller elements won't need to be compared with bigger elements ever in the future, thus time is saved. In addition, although we split the elements into 3 parts, pivot will be fixed after one iteration and only smaller and larger will be taken account into the next iteration. Hence the number of effective parts, which cost time next, is actually 2. How many times we can get smaller and larger then? O(logn) times, right? So at most we will have O(logn) iterations. Hence The time complexity of quicksort is O(nlogn).

Design

The key part of quicksort is partitioning, i.e., step 2 and 3. How can we do it? Again, let's design the process first without involving any coding details.

Say we have some elements 4, 1, 6, 3, 7. You don't have to write any code and you just need to manually partition them once like step 2 and 3. How will you do it in your imagination or on paper? Could you please try it now?

Done?

I bet you imagined or wrote down the flow similar as below:

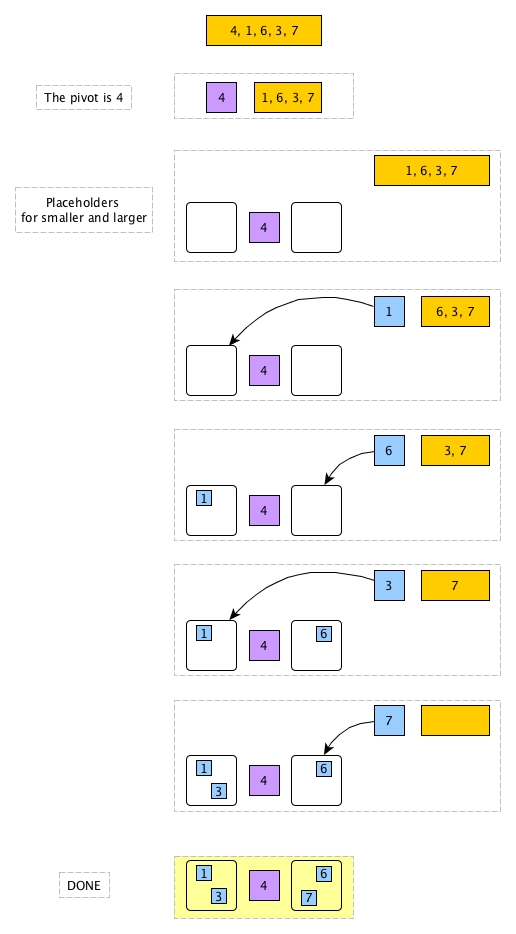
The mechanism of partition is not complicated. We get the pivot out first. Then get an element out of the rest of elements one by one. For each element, we compare it with the pivot. If it is smaller, then it goes to the left; otherwise, goes to the right. The whole process ends when no element remains. Simple enough? I believe even for non-developers, they would mannually do the partition like shown in the diagram.

Our design of partition is quite finished. It is time to implement it.

Imperative implementation

Let's first try using Java. Can we follow the design in the diagram directly? I bet not. The design assumed that the pivot 4 will have two bags (initially empty): one on its left and the other on its right. Just this single point beats Java. In Java or other imperative programming languages, normally when we sort some elements, all elements are in an array and we prefer doing things in place if we are able to. That says, for example, if we want 1 to be on the left hand side of 4, we would use swap. It is efficient and the correct way when adjusting the positions of elements in an array.

There are a number of ways to implement partition in Java and here the one presented in the book of Algorithms, Robert Sedgewick and Kevin Wayne is briefly presented as a diagram below:

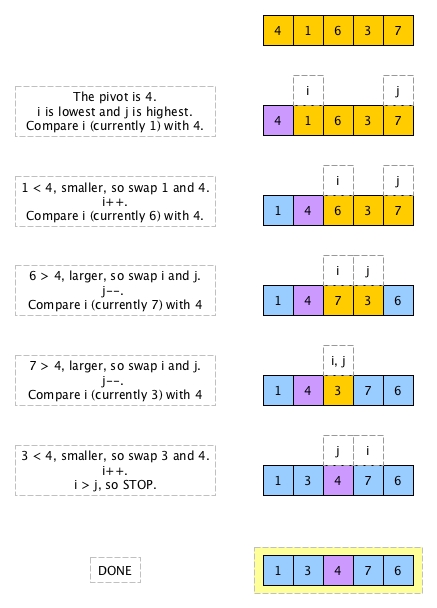
We do not have smaller bag or larger bag any more. We do not do throwing element into according bag either. We have to maintain two additional pointers i and j. i is used to indicate the next element in action. If an element is smaller than the pivot, swapping it with the pivot will put it to the left. If an element is larger, then we swap it with j's element. j can now decrease while i stays put because i now is a new element that was just swapped from j. The whole process stops when i > j.

As we can see, the implementation is quite different from the high level design and much more complicated, isn't it? The design just tells us we get a new element out, compare it with the pivot, and put it to the left or right depending on the comparison.. We cannot have such a simple summary for the implementation above. More than that, we need to pay extra attention on i and j as manipulating indices of an array is always error-prone.

The Java code is directly copied from the book to here:

private static int partition(Comparable[] a, int lo, int hi) {  
        int i = lo;
        int j = hi + 1;
        Comparable v = a[lo];
        while (true) { 
            // find item on lo to swap
            while (less(a[++i], v))
                if (i == hi) break;

            // find item on hi to swap
            while (less(v, a[--j]))
                if (j == lo) break;      // redundant since a[lo] acts as sentinel

            // check if pointers cross
            if (i >= j) break;

            exch(a, i, j);
        }

        // put partitioning item v at a[j]
        exch(a, lo, j);

        // now, a[lo .. j-1] <= a[j] <= a[j+1 .. hi]
        return j;
    }

Functional Implementation

The functional implementation fits the design perfectly and We have to thank the always creating new and deliver of functional programming style for that.

1. The design asks for two bags around the pivot and we can directly do that: (left, pivot, right).
2. The design says if an element is smaller, then put to the left. We can again directly do that if x < pivot then (x::left, pivot, right).
3. We can also directly handle larger: else (left, pivot, x::right).

For iterations, we can just use recursion. The complete OCaml code for partition is like this:

let partition pivot l =  
  (* we can actually remove pivot in aux completely.
     we put it here to make it more meaningful *)
  let rec aux (left, pivot, right) = function
    | [] -> (left, pivot, right)
    | x::rest ->
      if x < pivot then aux (x::left, pivot, right) rest
      else aux (left, pivot, x::right) rest
  in
  aux ([], pivot, []) l (* two bags are initially empty *)

If you know fold and remove pivot during the process, then it can be even simpler:

(* using the List.fold from Jane Street's core lib *)
let partition_fold pivot l =  
  List.fold ~f:(
    fun (left, right) x -> 
      if x < pivot then (x::left, right)
      else (left, x::right)) ~init:([], []) l

One we get the functional partition, we can write quicksort easily:

let rec quicksort = function  
  | [] | _::[] as l -> l
  | pivot::rest ->
    let left, right = partition_fold pivot rest in
    quicksort left @ (pivot::quicksort right)

Summary

Now we have two implementations for quicksort: imperative and functional. Which one is more straightforward and simpler?

In fact, functional style is more than just being consistent with the design: it handles data directly, instead of via any intermedia layer in between. In imperative programming, we often use array and like we said before, we have to manipulate the indices. The indices stand between our minds and the data. In functional programming, it is different. We use immutable list and using indices makes not much sense any more (as it will be slow). So each time, we just care the head element and often it is more than enough. This is one of the reasons why I love OCaml. Afterall, we want to deal with data and why do we need any unnecessary gates to block our way while they pretend to help us?

One may say imperative programming is faster as we do not need to constantly allocate memory for new things. Yes, normally array is faster than list. And also doing things in place is more effient. However, OCaml has a very good type system and a great GC, so the performance is not bad at all even if we always creating and creating.

If you are interested, you can do the design and imperative implementation for mergesort, and you will find out that we have to create new auxiliary spaces just like we would do in functional programming.

OCaml - the Hybrid

So far in this post, we used quite a lot of comparisons between imperative and functional to prove immutable is good and functional programming style is great. Yes, I am a fan of OCaml and believe functional programming is a decent way to do coding. However, I am not saying imperative programming is bad (I do Java and Python for a living in daytime and become an OCamler at deep night).

Imperative has its glories and OCaml actually never forgets that. That's why OCaml itself is a hybrid, i.e., you can just write OCaml code in imperative style. One of the reasons OCaml reserves imperative part is that sometimes we need to remember a state in one single place. Another reason can be that we need arrays for a potential performance boost.

Anyhow, OCaml is still a functional programming language and we should not forget that. Especially for beginners, please do pure functional programming in OCaml as much as possible. Do not bow to your imperative habit. For the question of when should I bring up imperative style in OCaml will be answered in the next post Mutable.

[1].

People enjoy flexbilities and conveniences, and that's one of the reasons why many people fancy Java and especially Python. It feels free there and we can easily learn them in 7 days and implement our ideas with them quickly. However, be aware of the double sides of being flexible and convenient.

When we really want to make a proper product using Java or Python, we may need to read books on what not to do even though they are allowed (yeah, this is a point, if we should not use something in most cases, why it is allowed at all?). We have to be very careful in many corners and 30% - 50% of the time would be spent on testing. Eventually, how to write beautiful code might become how to test beautifully.

OCaml and other functional programming languages are on the opposite side - they are very restrictive, but restrictions are for the great of good. For example, we cannot freely use the best excuse of sorry I can't return you a valid answer - return null;. Instead, we have the None, which is part of option, to explicitly tell you that nothing can be returned. The elegant reward of using option is that when we try to access it, we have to deal with the None. Thus NullPointerException does not exist in OCaml ([2]).

For if and pattern matching, OCaml forces us to cover all possible cases. It sounds troublesome during coding as we sometimes know that we don't care about some cases or some cases will never happen. Yes, we may ignore those cases in our working code in Java or Python, but later do we have to consider them in testing code? Often we do, right?

OCaml cuts off some flexibilities. As an outcome, to achieve a goal, we have quite limited number of ways and occasionally even just one way and that way might be very tough (we will see it in later posts on functional pearls). But trust me, after mastering OCaml at a certain level and looking at the very robust OCaml code you wrote, you would appreciate OCaml and recall this slogan:

"Less is more" - Andrea del Sarto, Robert Browning.

[2]. "Options are important because they are the standard way in OCaml to encode a value that might not be there; there's no such thing as a NullPointerException in OCaml. " - Chapter 1 in Real World Ocaml

Ps.

Wolverine in the head image of this post is a major character in X-Men's world. Since the regeneration of his body cells is super fast, he will not be permernantly hurt or age. Just like Wolverine, immutables in OCaml will not change once created. However, unlike Wolverine, they can not be immortals because many of them would be recycled by the garbage collector at some point during the runtime.