Heap - Leftist Tree

Heap is one of most important data structure, where the minimum of all elements can always be easily and efficiently retrieved.

Binary Heap

In imperative world, binary heap (implemented via array) is frequently used. Here is an example:

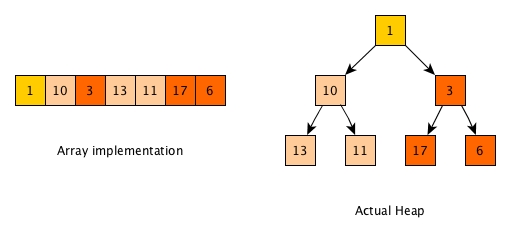
The (min) heap on the right hand side is a full binary tree indeed. The root is always the min and recursively, a root (of any sub tree) is always smaller than its two children. Note that we just need to keep partial order for heap, not total order like binary search tree. For example, 1 needs to be smaller than its two children, but the relationship between the two children does not matter. Thus, the left child and right child can be either 10 and 3 or 3 and 10. Moreover, the big node 17 can be in the right branch of 1 while its parent 3 is smaller than 10.

The array based implementation is actually beautiful. Essentially, it uses two tricks to simulate the binary heap tree:

1. If the index of a root is i, then its left child index is 2*i+1 and right child index is 2*i+2.
2. The relationship of left child and right child is not important, so the two child slots in the array for a root can be fully used. (Can we use array to implement a binary search tree?)

The time complexities on operations are:

1. get_min: O(1)
2. insert: O(logn)
3. delete_min: O(logn)
4. merge: O(n)

Although its merge is not satisfying, this data structure is adorable and gives us the most compact space usage on array.

However, unfortunately we cannot have it in pure functional world where mutable array is not recommended.

List based heap

I would like to first explore two possible functional approaches for heap (the list based in this section and the direct binary tree based in next section) . They are trivial or even incomplete, but the ideas behind may lead to the invention of leftist tree.

List is basically the replacement of array in functional world and of course, we can use it for heap. The idea is simple:

1. When insert x, linearly compare x with all existing elements one by one and insert it to the appropriate place where the element on its left hand side is smaller and the element on its right is equal or bigger.
2. When get_min, it is as simple as returning the head.
3. When delete_min, remove the head.
4. When merge, do a standard merge like in mergesort.

The time complexities are:

1. get_min: O(1)
2. insert: O(n)
3. delete_min: O(1)
4. merge: O(n)

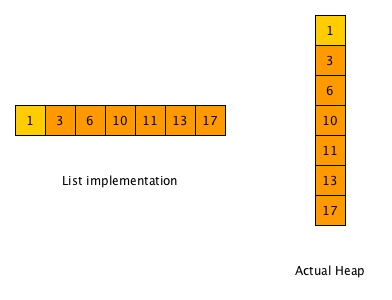
We can see that in this design, the list is fully sorted all the time. And also it is a tree, with just one branch always.

Of course, the performance of insert and merge is O(n) which is unacceptable. This is due to the adoption of just one leg which is crowded with elements and all elements have to be in their natural order to fit in (remember a parent must be smaller than its kid(s)?). Eventually the fact of total order is not necessary is not leveraged at all.

Hence, we need at least two branches so that we may be able to spread some elements into different branches and the comparisons of the children of a root may be avoided.

Binary Heap not using array

Since the array based binary heap is a binary tree, how about implementing it directly in a binary tree form?

We can define a binary tree heap like this:

type 'a bt_heap_t =  
  | Leaf
  | Node of 'a * 'a bt_heap_t * 'a bt_heap_t

The creation of the type is easy, but it is hard to implement those operations. Let's take insert as an example.

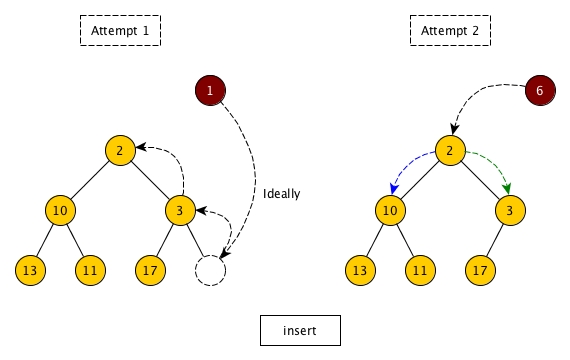
The attempt 1 in the diagram above illustrates the idea behind the array based binary heap. When we insert an element, ideally we should put it in the last available place at the bottom level or the first place at a brand new level if already full, then we do a pull up by comparing and swapping with parents one by one. Obviously, we cannot do it in a pure tree structure since it is not efficient to find the initial place.

So let's try attempt 2 by directly try to insert from top to bottom. So in the example, 2 < 6 so 2 stays and 6 should continue going down. However, the question now is which branch it should take? 10 or 3? This is not trivial to decide and we have to find a good rule.

We will also have problem in delete_min.

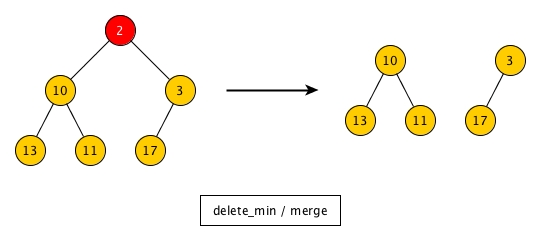
If we delete the root (min), then we will have two binary trees. Then the question is how to merge them? Do we just take all elements of one of the trees, and insert every element into the other tree? Will this way be efficient even if we are able to design a good insert?

If we consider insert as merge with a single node tree, then the problem of insert becomes the problem of merge, just like delete_min. Should we design a good merge so that both insert and delete_min are naturally solved?

Bear all those questions in mind, and now we can start look at leftist tree.

Leftist Tree

The concerns in answering those questions in the previous section are majorly about the performance. We are dealing with a tree. How the tree getting structure or transformed along the time is very important and it affects the performance a lot.

For example, for the question of which branch to take when inserting, if we just always go left, then the left branch will be longer and longer if we insert lots of elements, and the time complexity becomes O(n).

Also when merging, the two trees are already heaps, i.e., the elements and structure of either tree obeys the principle that a parent must be smaller than its children. Why do we need to destory one tree completely? Why not try to keep the structures of two trees untouched as much as possible? If we can somehow attach a root from one tree directly under a root of another tree, then all children under the first root can stay still and no operations are necessary for them.

Let's see how leftist tree is designed to make sure the good performance.

Left always longer

Leftist tree always keeps the left branches of all roots being the longer and in worst case, they are as long as the right branches. In other word, all right branches of all roots are shortest. This makes sense. When we decide which branch to go, if we know one branch is always shorter than the other, then we should take it. This is because shorter branch means potentially less nodes and the number of future possible operations intends to be smaller.

In order to maintain this property, each node has a rank, which indidates the length of the path between the node and the right most leaf. For example,

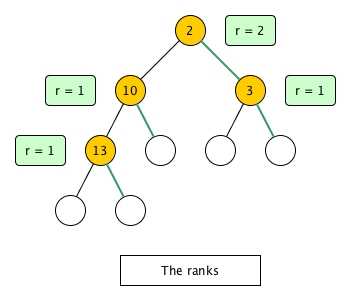
The way of keep ranks up-to-date is like this:

1. We always assume the rank of the right child <= the rank of the left child.
2. So we always go right.
3. If we reach a leaf, then we replace the leaf with our element and update the ranks of all the parents back to the root. Note that the element in this context is not necessarily the original new element which is being inserted and we will explain it soon.
4. When updating the rank of a parent, we first compare the rank of left rank_left and the rank of right rank_right. If rank_left < rank_right, then we swap the left child and the right child and update the rank of the parent to be rank_left + 1; other wise rank_right + 1

A diagram is better than hundreds of words. Let's build a leftist by inserting two elements.

Insert

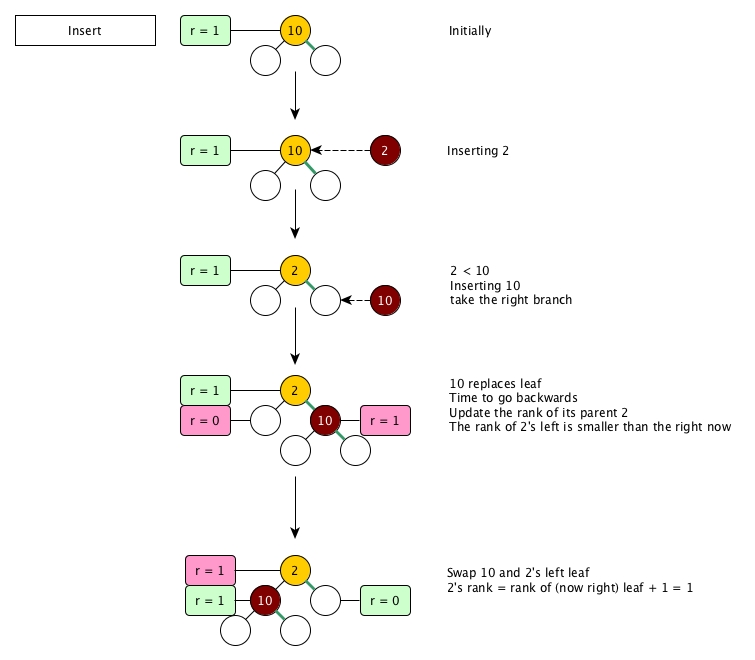
We can see that by always putting the higher rank to the left can make the right branch being shortest all the time. Actually, this strategy is how this design of tree based heap got the name leftist, i.e., more nodes intend to be on the left side.

But this is not the full story of leftist. Actually, although the diagram above describes insert, it is just for the purpose of demonstration of how ranks are updated.

In leftist tree, the most important operation is merge and an insert is just a merge with a singleton tree that has only the new element and two leaves.

Merge

Merge is a recursive operation.

1. We have two trees to merge: merge t1 t2.
2. Compare two roots, if k1 > k2, we simply switch two trees by merge t2 t1. This is to make sure the tree on the left always has smaller key, for conveniences.
3. Since t1 has smaller key, its root should stay as the new root.
4. Because t1's right branch r is always shortest, we then do merge r t2.
5. If one of the two trees is leaf, we simply returns the other. And begin the rank updating process back to the root.
6. The rank updating is the same as we described in the previous section.

Again, let's see an example.

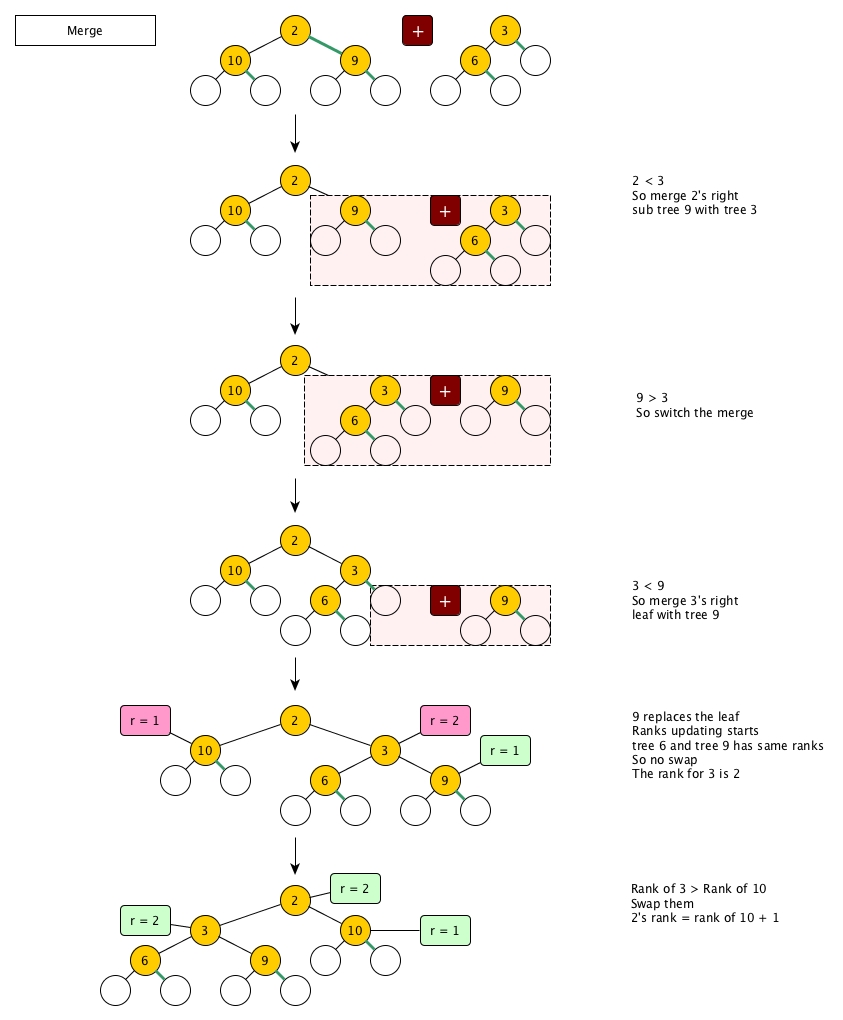
Code

type

type 'a leftist =  
  | Leaf 
  | Node of 'a leftist * 'a * 'a leftist * int

essentials

let singleton k = Node (Leaf, k, Leaf, 1)

let rank = function Leaf -> 0 | Node (_,_,_,r) -> r  

merge

let rec merge t1 t2 =  
  match t1,t2 with
    | Leaf, t | t, Leaf -> t
    | Node (l, k1, r, _), Node (_, k2, _, _) ->
      if k1 > k2 then merge t2 t1 (* switch merge if necessary *)
      else 
        let merged = merge r t2 in (* always merge with right *)
        let rank_left = rank l and rank_right = rank merged in
        if rank_left >= rank_right then Node (l, k1, merged, rank_right+1)
        else Node (merged, k1, l, rank_left+1) (* left becomes right due to being shorter *)

insert, get_min, delete_min

let insert x t = merge (singleton x) t

let get_min = function  
  | Leaf -> failwith "empty"
  | Node (_, k, _, _) -> k

let delete_min = function  
  | Leaf -> failwith "empty"
  | Node (l, _, r, _) -> merge l r

Time complexity

1. get_min: O(1)
2. insert: O(logn)
3. delete_min: O(logn)
4. merge: O(logn)

Leftist tree's performance is quite good. Comparing to the array based binary heap, it has a much better merge. Moreover, its design and implementation are simple enough. Thus, leftist tree can an excellent choice for heap in the functional world.