Recursive Memoize & Untying the Recursive Knot

When I wrote the section of When we need later substitution in Mutable, I struggled. I found out that I didn't fully understand the recursive memoize myself, so what I had to do was just copying the knowledge from Real World OCaml. Luckily, after the post was published, glacialthinker commented in reddit:
(I never thought before that a recursive function can be split like this, honestly. I don't know how to induct such a way and can't explain more. I guess we just learn it as it is and continue. More descriptions of it is in the book.)
This is "untying the recursive knot". And I thought I might find a nice wikipedia or similiar entry... but I mostly find Harrop. :) He actually had a nice article on this many years back in his OCaml Journal. Anyway, if the author swings by, searching for that phrase may turn up more material on the technique.
It greatly enlightened me. Hence, in this post, I will share with you my futher understanding on recursive memoize together with the key cure untying the recursive knot that makes it possible.
Simple Memoize revamped
We talked about the simple memoize before. It takes a non-recursive function and returns a new function which has exactly the same logic as the original function but with new new ability of caching the argument, result pairs.
let memoize f =
let table = Hashtbl.Poly.create () in
let g x =
match Hashtbl.find table x with
| Some y -> y
| None ->
let y = f x in
Hashtbl.add_exn table ~key:x ~data:y;
y
in
g
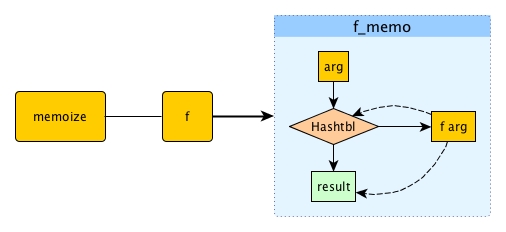
The greatness of
memoizeis its flexibility: as long asftakes a single argument,memoizecan make a memo version out of it without touching anything insidef.
This means while we create f, we don't need to worry about the ability of caching but just focus on its own correct logic. After we finish f, we simply let memoize do its job. Memoization and functionality are perfectly separated.
Unfortunately, the simple memoize cannot handle recursive functions. If we try to do memoize f_rec, we will get this:
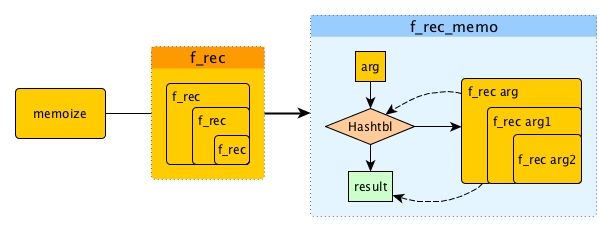
f_rec is a recursive function so it will call itself inside its body. memoize f_rec will produce f_rec_memo which is a little similar as the previous f_memo, yet with the difference that it is not a simple single call of f_rec arg like we did f arg. Instead, f_rec arg may call f_rec again and again with new arguments.
Let's look at it more closely with an example. Say, arg in the recursive process will be always decreased by 1 until 0.
- Let's first od
f_rec_memo 4. f_rec_memowill check the4againstHashtbland it is not in.- So
f_rec 4will be called for the first time. - Then
f_rec 3,f_rec 2,f_rec 1andf_rec 0. - After the 5 calls, result is obtained. Then 4, result pair is stored in
Hashtbland returned. - Now let's do
f_rec_memo 3, what will happen? Obviously,3won't be found inHashtblas only4is stored in step 5. - But should 3, result pair be found? Yes, it should of course because we have dealt with
3in step 4, right? - Why
3has been done but is not stored? - ahh, it is because we did
f_rec 3but notf_rec_memo 3while only the latter one has the caching ability.
Thus, we can use memoize f_rec to produce a memoized version out of f_rec anyway, but it changes only the surface not the f_rec inside, hence not that useful. How can we make it better then?
Recursive Memoize revamped
What we really want for memoizing a recursive function is to blend the memo ability deep inside, like this:
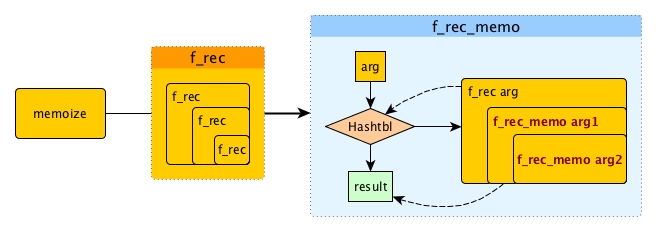
Essentially we have to replace f_rec inside with f_rec_memo:
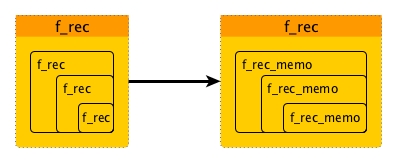
And only in this way, f_rec can be fully memoized. However, we have one problem: **it seems that we have to change the internal of f_rec.
If we can modify f_rec directly, we can solve it easily . For instance of fibonacci:
let rec fib_rec n =
if n <= 1 then 1
else fib_rec (n-1) + fib_rec (n-2)
we can make the memoized version:
let fib_rec_memo_trivial n =
let table = Hashtbl.Poly.create () in
let rec fib_rec_memo x =
match Hashtbl.find table x with
| Some y -> y
| None ->
let y = fib_rec_memo (x-1) + fib_rec_memo (x-2) in
Hashtbl.add_exn table ~key:x ~data:y;
y
in
fib_rec_memo
In the above solution, we replaced the original fib_rec inside with fib_rec_memo, however, we also changed the declaration to fib_rec_memo completely. In fact, now fib_rec is totally ditched and fib_rec_memo is a new function that blends the logic of memoize with the logic of fib_rec.
Well, yes, fib_rec_memo_trivial can achieve our goal, but only for fib_rec specificly. If we need to make a memoized version for another recursive function, then we need to change the body of that function again. This is not what we want. We wish for a memoize_rec that can turn f_rec directly into a memoized version, just like what the simple memoize can do for f.
So we don't have a shortcut. Here is what we need to achieve:
- we have to replace the
f_recinside the body off_recwithf_rec_memo - We have keep the declaration of
f_rec. - We must assume we can't know the specific logic inside
f_rec.
It sounds a bit hard. It is like giving you a compiled function without source code and asking you to modify its content. And more imporantly, your solution must be generalised.
Fortunately, we have a great solution to create our memoize_rec without any hacking or reverse-engineering and untying the recursive knot is the key.
Untying the Recursive Knot
To me, this term sounds quite fancy. In fact, I never heard of it before 2015-01-21. After I digged a little bit about it, I found it actually quite simple but very useful (this recursive memoize case is an ideal demonstration). Let's have a look at what it is.
Every recursive function somehow follows a similar pattern where it calls itself inside its body:
Once a recursive function application starts, it is out of our hands and we know it will continue and continue by calling itself until the STOP condition is satisfied. What if the users of our recursive function need some more control even after it gets started?
For example, say we provide our users fib_rec without source code, what if the users want to print out the detailed trace of each iteration? They are not able unless they ask us for the source code and make a new version with printing. It is not that convenient.
So if we don't want to give out our source code, somehow we need to reform our fib_rec a little bit and give the space to our users to insert whatever they want for each iteration.
let rec fib_rec n =
if n <= 1 then 1
else fib_rec (n-1) + fib_rec (n-2)
Have a look at the above fib_rec carefully again, we can see that the logic of fib_rec is already determined during the binding, it is the fib_recs inside that control the iteration. What if we rename the fib_recs within the body to be f and add it as an argument?
let fib_norec f n =
if n <= 1 then 1
else f (n-1) + f (n-2)
(* we actually should now change the name of fib_norec
to something like fib_alike_norec as it is not necessarily
doing fibonacci anymore, depending on f *)
So now fib_norec won't automatically repeat unless f tells it to. Moreover, fib_norec becomes a pattern which returns 1 when n is <= 1 otherwise add f (n-1) and f (n-2). As long as you think this pattern is useful for you, you can inject your own logic into it by providing your own f.
Going back to the printing requirement, a user can now build its own version of fib_rec_with_trace like this:
let rec fib_rec_with_trace n =
Printf.printf "now fibbing %d\n" n;
fib_norec fib_rec_with_trace n
Untying the recusive knot is a functional design pattern. It turns the recursive part inside the body into a new parameter
f. In this way, it breaks the iteration and turns a recursive function into a pattern where new or additional logic can be injected into viaf.
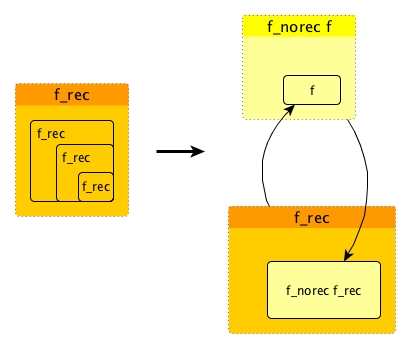
It is very easy to untie the knots for recusive functions. You just give an addition parameter f and replace f_rec everywhere inside with it. For example, for quicksort:
let quicksort_norec f = function
| [] | _::[] as l -> l
| pivot::rest ->
let left, right = partition_fold pivot rest in
f left @ (pivot::f right)
let rec quicksort l = quicksort_norec quicksort l
There are more examples in Martin's blog, though they are not in OCaml. A formalized description of this topic is in the article Tricks with recursion: knots, modules and polymorphism from The OCaml Journal.
Now let's come back to recursive memoize problem with our new weapon.
Solve Recursive Memoize
At first, we can require that every recursive function f_rec must be supplied to memoize_rec in the untied form f_norec. This is not a harsh requirement since it is easy to transform f_rec to f_norec.
Once we get f_norec, we of course cannot apply memoize (non-rec version) on it directly because f_norec now takes two parameters: f and arg.
Although we can create f_rec in the way of let rec f_rec arg = f_norec f_rec arg, we won't do it that straightforward here as it makes no sense to have an exactly the same recursive function. Instead, we can for now do something like let f_rec_tmp arg = f_norec f arg.
We still do not know what f will be, but f_rec_tmp is non-recursive and we can apply memoize on it: let f_rec_tmp_memo = memoize f_tmp.
f_rec_tmp_memo now have the logic of f_norec and the ability of memoization. If f can be f_rec_tmp_memo, then our problem is solved. This is because f is inside f_norec controlling the iteration and we wished it to be memoized.
The magic that can help us here is making f mutable. Because f needs to be known in prior and f_rec_tmp_memo is created after, we can temporarily define f as a trivial function and later on after we create f_rec_tmp_memo, we then change f to f_rec_tmp_memo.
Let's use a group of bindings to demonstrate:
(* trivial initial function and it should not be ever applied in this state *)
let f = ref (fun _ -> assert false)
let f_rec_tmp arg = f_norec !f arg
(* memoize is the simple non-rec version *)
let f_rec_tmp_memo = memoize f_rec_tmp
(* the later substitution made possible by being mutable *)
f := f_rec_tmp_memo
The final code for memoize_rec is:
let memo_rec f_norec =
let f = ref (fun _ -> assert false) in
let f_rec_memo = memoize (fun x -> f_norec !f x) in
f := f_rec_memo;
f_rec_memo